Dataviz et relations entre les données : attention aux pièges

Parfois, vous tombez sur un joli diagramme qui vous explique en quoi deux éléments apparemment sans relation sont liés par une obscure courbe de tendances identiques.

Ce fut le cas récemment sur Twitter, où j’ai découvert cette visualisation : Internet Explorer vs Murder Rate (US). Alors oui, j’ai souri trois secondes, le temps de me rendre compte que cette dataviz était une tromperie – pour la blague, certes, mais quand même.

Une question d’échelle(s) et de référentiel(s)

Pour comprendre le souci, j’ai fait le petit calcul suivant : si 18000 meurtres (ce qui n’est pas un taux, au passage mais un nombre arbitraire) représentent 90% (comme pour l’axe de valeur du taux pour IE), alors que représentent 14000 meurtres ? Sur le diagramme, 30%, mais avec le calcul suivant : 90* 14000 / 18000 = 70 : un écart de 40% se serait donc glissé dans ce diagramme ?

Le premier problème donc, c’est d’avoir deux axes qui ne sont pas réellement en relation. Pour résoudre ce premier problème, je vous propose le diagramme suivant :

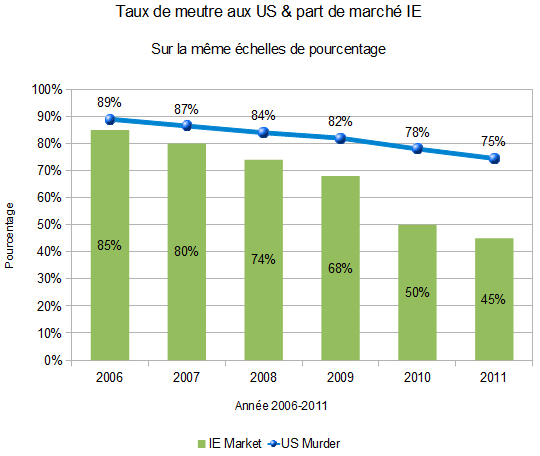Tout de suite, ce n’est plus tout à fait la même chose. Vous pouvez constater que la courbe des meurtres aux USA n’a pas tout à fait la même tête que la descente des parts de marché d’Internet Explorer (il chute plus vite que le taux de meurtres).

Pour obtenir ce diagramme, j’ai évalué (un peu à la louche je l’admets) le nombre de meurtre et le % d’IE, j’ai ensuite transformé en pourcentage (selon la formule précédemment citée) pour obtenir le taux de meurtres à la place des chiffres (18000, etc.).

Mais cette dataviz aussi est incorrecte ! Parce qu’elle essaye de comparer deux choses qui n’ont rien à voir pour commencer. Certes, l’échelle est plus intéressante, mais ne permet toujours pas de répondre à la question de la relation entre les deux données.

D’ailleurs, chose amusante, si je demande à mon tableur de représenter les deux échelles sur deux axes différents, voici ce que j’obtiens :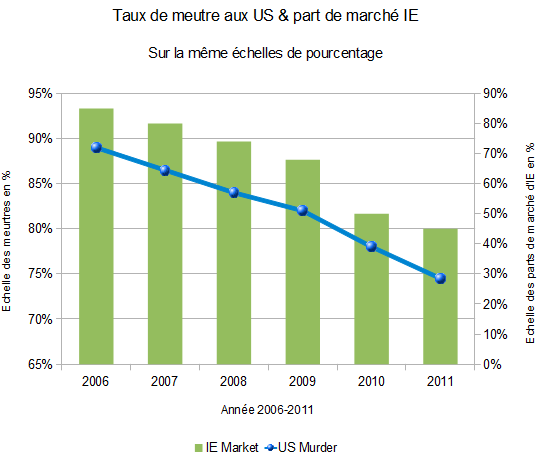

Comparer ce qui est comparable

Lorsque vous étiez à l’école un professeur a dû vous expliquer que comparer des Poires et des Pommes, ça ne donnait pas de très bon résultat (à propos des comparaisons de fractions, de mémoire). Et là, c’est exactement la même chose !

Voici les deux types de données ici présentées :

Une quantité fixe : le nombre de meurtres.
Un ratio : la part de marché d’Internet Explorer.

Autant dire que ces deux données ne peuvent pas être comparée telle qu’elles sont ! Si quelqu’un cherche à savoir s’il y a une relation entre le nombre de meurtres et la part d’IE, il faudrait d’abord transformer un peu tout ça en quelque chose de comparable.

Qu’est-ce qui est comparable ?

Il y a un tas de façon de comparer deux données différentes, mais je ne suis pas sûr que toutes soient pertinentes. Je vais essayer d’en présenter une et nous verrons ensuite si ça veut dire quelque chose.

Tout d’abord, je reviens aux données sur IE : ce sont des parts de marché. En gros, c’est le pourcentage de gens utilisant le logiciel. Il est plutôt difficile de trouver le même genre de comparaison pour les meurtres : faut-il prendre le nombre total de décès comme référence ? Le nombre de personnes que cela représente par rapport à la population globale ?

Tout dépend ce que l’on cherche à savoir : est-ce que la proportion de décès par meurtre a augmenté ? Ou est-ce que la proportion de meurtres a augmenté par rapport à la population totale ?

Je vais choisir de faire une comparaison avec la population totale, ce qui m’arrange plutôt bien, puisque sur Wikipédia il y a quelques statistiques à ce sujet : Classement des pays par taux d’homicide volontaire. Je sais, il y a plus drôle comme données, mais je fais avec ce que j’ai sous la main.

En outre, je ne vais pas comparer les deux données : je vais faire le ratio entre chaque valeur à la même année. Si la tendance est la même entre les deux, alors je dois obtenir une ligne droite : si le ratio est différent, cela implique qu’une valeur change plus qu’une autre (en plus ou en moins).

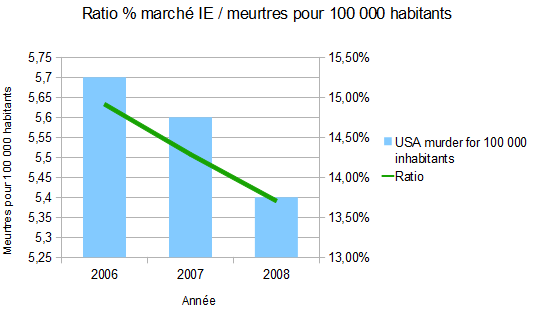
Et voilà ! J’annonce fièrement que… et bien rien en fait. J’ai seulement tracé un diagramme avec une ligne qui plonge, mais ça ne veut rien dire du tout en réalité.

Tout ceci ne prouve rien

Vous avez vu mon précédent diagramme, et vous vous êtes dit : « c’est la preuve qu’il n’y a aucun rapport entre les données ! ».

En fait, ce n’est pas vrai. Plus précisément : ceci ne permet pas d’affirmer ou d’infirmer la relation. Ce n’est pas vraiment pertinent.

Si vous regardez bien, j’ai placé l’échelle du ratio à droite, qui va de 13% à 15.5%. En somme, 2.5 points séparent le maximum du minimum. Je n’ai pas non plus affiché la valeur de chaque ratio. Tout ce que vous pouvez voir c’est une ligne qui plonge. Que se serait-il passé si j’avais choisi une autre échelle, allant, par exemple, de 0 à 100% ? Vous auriez vu plutôt une ligne droite – ce qui aurait alors indiqué exactement le message inverse de mon diagramme !

C’est là qu’est le piège : lorsque vous choisissez des échelles et des représentations, vous orientez la vision de l’observateur vers le message qui vous intéresse, que vous en soyez conscient ou non. Au passage, le premier observateur, c’est vous-même !

Il faut faire attention : même en essayant de comparer ce qui peut l’être a priori, vous pouvez avoir des surprises.

Attention aux visualisations

Le but n’était pas de démontrer que la blague d’origine n’est qu’une (bonne) blague : tout le monde doit pouvoir s’en rendre compte en réfléchissant un peu.

Non, mon but ici était plutôt ceci :

Faire comprendre qu’une visualisation de données, c’est sortir de la donnée brute et aller vers de l’analyse.
Montrer que les relations entre les données sont très complexes à démontrer.

Ce n’est pas vraiment une surprise pour les connaisseurs et les analystes en la matière, mais c’est un piège très fréquent, et dans lequel il est facile de tomber. C’est l’un des problèmes le plus fréquent d’ailleurs lorsque vous regardez les sites d’informations ou la TV : des visualisations avec des données de types et d’origines très différents, des échelles trompeuses, etc.

En outre, il faut rester vigilant : parfois, nous voyons des relations entre les données parce que nous voulons les y trouver (nous sommes le premier observateur). Pourtant, un travail de fond et des analyses supplémentaires sont toujours nécessaires pour trouver et décortiquer les relations entre les données.

C’est, à mon avis, un argument important pour favoriser la culture de la donnée, et une plus large éducation et sensibilisation du public (dès l’enfance), aux visualisations et aux traitements des données.